確率統計：モンテカルロ

モンテカルロ計算を考えてみます。

統計を含め、科学技術計算には、numpyが使えます。
行列操作ができ、乱数や確率に関するライブラリが豊富です。
numpyは数値計算用のライブラリであり、
中身の逆行列計算などのアルゴリズムはCなどで書かれています。
そのため、うまく書けばpythonとは言えども高速な計算が可能です。

モンテカルロと言うのはモナコにある町の名前です。
計算機科学の世界でいういわゆるモンテカルロ法というのは確率的なサンプリングを行うことによって、計算を行うことを指し、
フォンノイマンによって命名されたと言われています。

今回はnumpyで簡単なモンテカルロ計算を行います。

numpyをまずimportします。
import numpy

中心０分散１の正規乱数を発生させるには、

x = numpy.random.randn(10000)

とします。

同一正規分布に従う二つの独立な変数x1,x2があったとします。
常にx1<x2であるという制約があった場合、この二つはどのような分布となるでしょうか。

x1 = numpy.random.randn(10000)
x2 = numpy.random.randn(10000)
index = x1 < x2

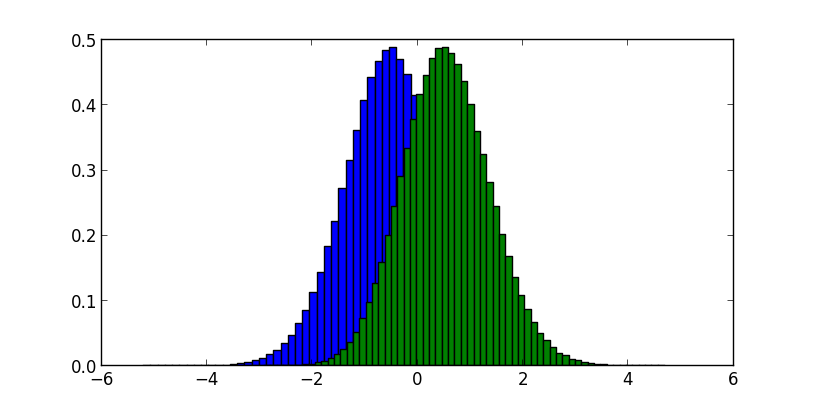
x1とx2をプロットすると

この場合、切断正規分布という分布になります。
こうするとx1とx2は独立ではなくなり、p(x1,x2)と書くと、x1の確率は

p(x1) = ∫p(x1,x2) dX2

となります。
x1とx2のヒストグラムをとるとこんな感じです。

このようにサンプリングを通して、面積や分布などを調べることをモンテカルロ法といいます。
よく円の面積などの例が教科書などに載っていると思います。
モンテカルロは概念が簡単で容易に理解できますが、奥が深いです。


プロットはmatplotlibを使いました。
matplotlibについてはまたそのうちレポートします。