sampling

あるとき、統計分析のため、
重みに応じたリサンプリングをする必要ができました。


floatのベクトルvがあったとすると

p=v/sum(v)

を確率ベクトルとして、復元抽出するコードを考えてみました。
探しては見たのですが、すぐには見つかりませんでした。
そこで、したのような処理で実現してみました。

import numpy as np

n = 100
def resamp( v, n ):
   vsum = np.sum(v)
   vcum = np.cumsum(v)
   indices = np.array([ np.argmax(1.0/(vcum - r)) for r in np.random.uniform(0,vsum,n) ])
   return indices


確率ベクトルvと出力サンプル数nを入力し、インデックスのnumpy.arrayを返す関数です。

備忘録のため、ブログに載せてみましたが、
関数一つでできる方法がないのだろうか。

regression OLS

pythonで回帰分析(regression)を行うことができます

回帰分析は古くから知られており、汎用的で世間で一番用いられている統計分析法かもしれません。
回帰分析というのは、簡単に言うならば、説明変数から目的変数をダイレクトに計算する線形式を決めることと言えます。
もちろん、その間に因果関係がなさそうなデータでも、入力（説明）変数と出力（目的）変数のデータさえそろえば、計算できます。 なので、風の風速と桶（おけ）店の振り上げの関係式も分析できます。

推定性能についてはR二乗値などの値で評価します。 ここでは「通常の方法」についてpythonで行う方法についてご紹介します。 OLS法というのはOrdinary Least Square（普通最小二乗法）です。 回帰分析は最小二乗法で「行うべきもの」と考えている人もいるかもしれませんが、 他にもいくつか選択肢はあります。 例えば、重み付き最小二乗とか、ロバスト推定とか。 なので、一番使われている「通常の方法」がOrdinary Least Squareです。

import numpy
import statsmodels.formula.api as sfa
d = {'x':numpy.random.randn(10,3), 'y':numpy.random.randn(10) }
o = sfa.ols( 'y~x', data=d )
r = o.fit()
print r.summary()

もし、上のコードでstatsmodelsが無いと言われたら、 easy_installで入れてください。 結果の表示は下のようになりました。

                            OLS Regression Results
==============================================================================
Dep. Variable:                      y   R-squared:                       0.403
Model:                            OLS   Adj. R-squared:                  0.104
Method:                 Least Squares   F-statistic:                     1.348
Date:                Sat, 14 Nov 2015   Prob (F-statistic):              0.345
Time:                        23:01:08   Log-Likelihood:                -13.518
No. Observations:                  10   AIC:                             35.04
Df Residuals:                       6   BIC:                             36.25
Df Model:                           3
Covariance Type:            nonrobust
==============================================================================
                 coef    std err          t      P>|t|      [95.0% Conf. Int.]
------------------------------------------------------------------------------
Intercept      1.2127      0.745      1.628      0.155        -0.610     3.035
x[0]           0.6436      0.379      1.697      0.141        -0.284     1.572
x[1]          -1.1225      0.837     -1.341      0.229        -3.171     0.926
x[2]          -1.2621      1.742     -0.724      0.496        -5.526     3.001
==============================================================================
Omnibus:                        0.620   Durbin-Watson:                   1.691
Prob(Omnibus):                  0.733   Jarque-Bera (JB):                0.417
Skew:                          -0.425   Prob(JB):                        0.812
Kurtosis:                       2.472   Cond. No.                         8.32
==============================================================================

Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly
 specified.

出力がたくさんありすぎて、わからなくなってしまうかもしれません。 真ん中の少し下辺りに係数(x[*] coef)や切片(Intercept coef)の推定値が表示されています。
あとはAIC・BICや基本統計量が表示されています。 AIC・BICは値が低いほうがよりデータに近いことを示す情報量規準というものです。 それぞれの統計量についてはまた回を改めて説明します。 回帰分析関数クラスのolsへ入力する'y~x'というのはGNU Rと同様の書式です。 つまり、この場合、ｙが目的変数で右側のxが説明変数です。

回帰分析や検定については他をググってみてください。 もっと詳しく丁寧に書いてあるページがたくさんあります。

数理統計学・データサイエンスとpython

pythonを使って統計アルゴリズムを記述することができます。
現在、統計アルゴリズムをコーディングする上でいくつかの比較的簡便な方法が開発されてきました。統計言語Sを基にしたR言語もその一つです。

ここでは最近急速に発展してきたpythonを使った方法について考察してみます。
最近の流れとしては大規模データ、いわゆるビッグデータの分析に注目が集まっているようです。
pythonはこれまでにも書いてきたようにスクリプト言語で基本インタプリタですので、書き方によっては計算時間がネックになってしまうことがあります。
さらには、もともと統計分析を目的として開発されたSまたはR言語のような機能の豊富さには負けます。
しかし、pythonはそれを上回るほどの開発効率やソースコードの簡潔さが特徴で、ライブラリも多岐にわたるため応用範囲が広いという利点があります。

科学技術計算で使うためのライブラリとしては、有名なものだけでも

• Numpy
• Scipy
• Sklearn
• Pandas
• Jubatus

などがあります。

Numpyについてはこれまでも何回か説明してきましたが、統計に限らず数値演算の基本的な機能を提供します。
Numpyのもっとも重要な機能はArrayだと思います。
Arrayというのはつまり配列ですが、python標準のlistより、ベクトル的な計算を意識したもので、これを効果的に使うことにより、効率的な計算が可能です。
NumpyにはMatrixという型もあります。
Matrixを使うと行列演算が簡単にかけるので便利ではありますが、
Arrayの方が使い勝手が良いと思います。


ScipyはNumpyではカバーしきれなかった科学技術寄りの機能を実現しています。
たとえば、統計アルゴリズムの例でいうと、乱数発生はNumpyの機能が使えます。つまり、
numpy.random.randn(100)
などとすると100個の正規乱数がnumpy.array形式で生成されます。
しかし、正規分布の確率密度関数のグラフが書きたいとなれば、
scipy.statsの機能が使えます。

import numpy
import scipy.stats
p = scipy.stats.norm.pdf( numpy.arange(-3,3,0.1) )

とすれば、pに-3から3までの正規密度関数の値が入ります。
正規分布のほかにもcauchy分布やgammaやvon misesなどの分布もあります。
統計の論文に出てきそうな標準的確率分布はあらかたあります。


残りのライブラリの説明はまた今度します。
興味があれば、それぞれググってみてください。

確率統計：モンテカルロ

モンテカルロ計算を考えてみます。

統計を含め、科学技術計算には、numpyが使えます。
行列操作ができ、乱数や確率に関するライブラリが豊富です。
numpyは数値計算用のライブラリであり、
中身の逆行列計算などのアルゴリズムはCなどで書かれています。
そのため、うまく書けばpythonとは言えども高速な計算が可能です。

モンテカルロと言うのはモナコにある町の名前です。
計算機科学の世界でいういわゆるモンテカルロ法というのは確率的なサンプリングを行うことによって、計算を行うことを指し、
フォンノイマンによって命名されたと言われています。

今回はnumpyで簡単なモンテカルロ計算を行います。

numpyをまずimportします。
import numpy

中心０分散１の正規乱数を発生させるには、

x = numpy.random.randn(10000)

とします。

同一正規分布に従う二つの独立な変数x1,x2があったとします。
常にx1<x2であるという制約があった場合、この二つはどのような分布となるでしょうか。

x1 = numpy.random.randn(10000)
x2 = numpy.random.randn(10000)
index = x1 < x2

x1とx2をプロットすると

この場合、切断正規分布という分布になります。
こうするとx1とx2は独立ではなくなり、p(x1,x2)と書くと、x1の確率は

p(x1) = ∫p(x1,x2) dX2

となります。
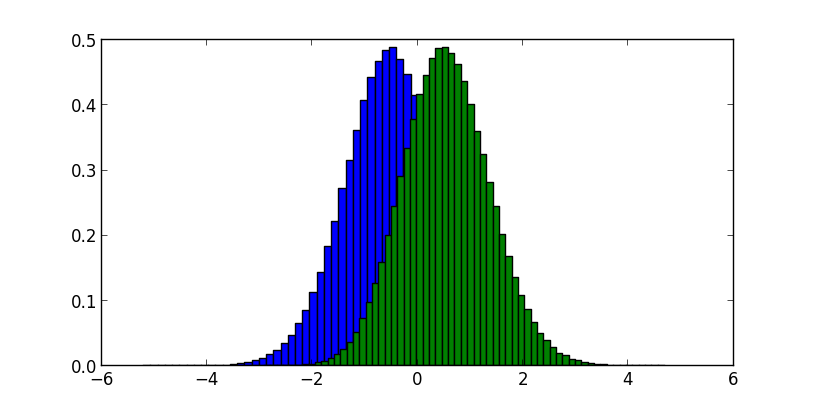
x1とx2のヒストグラムをとるとこんな感じです。

このようにサンプリングを通して、面積や分布などを調べることをモンテカルロ法といいます。
よく円の面積などの例が教科書などに載っていると思います。
モンテカルロは概念が簡単で容易に理解できますが、奥が深いです。


プロットはmatplotlibを使いました。
matplotlibについてはまたそのうちレポートします。